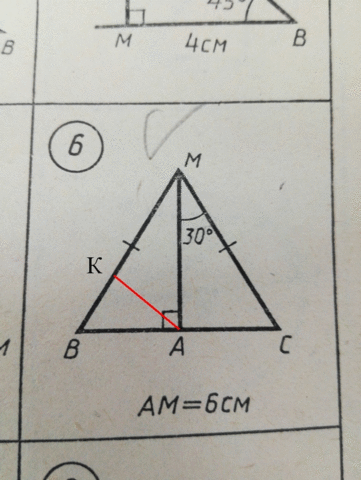
В равнобедренном ΔВМС высота АМ является и медианой и биссектрисой.
Биссектриса АМ разделила ∠ВМС пополам, т.е.
∠ВМА = ∠АМС = 30°
В прямоугольном ΔАМВ катет АВ, лежащий против угла в 30°, равен половине гипотенузы МВ, значит,
х см = АВ
2х см - МВ
По теореме Пифагора
МВ² = АВ² + АМ²
(2х)² = х² + 6²
4х² - х² = 36
3х² = 36
х² = 36 : 3
х² = 12
х = √12 = 2√3
АВ = 2√3 см
МВ = 2 · 2√3 = 4√3 см
2)
Расстояние от точки до прямой - это перпендикуляр, опущенный из этой точки к данной прямой, т.е. и АК ⊥ ВМ.
ΔМВА подобен ΔКВА, т.к. у них:
∠В - общий
∠МАВ = ∠АКВ = 90°
Получим пропорцию из подобных сторон:
МА : ВМ = АК : АВ
6 : 4√3 = АК : 2√3
АК = 6 · 2√3 : 4√3 = 3см
Ответ: 3 см