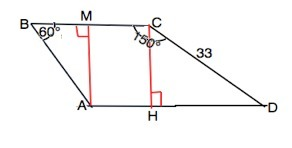
Основания трапеции параллельны, поэтому при их пересечении с боковыми сторонами сумма внутренних углов равна 180°
Угол CDA=180°-150°=30°
Опустив высоту СН, получим прямоугольный треугольник СНВ, в котором катет СН противолежит углу 30°
СН= CD:2=16,5
Высоты трапеции равны. АМ=СН=16,5
АВ=АМ:sin MBA=16,5:(√3/2)

------------
Ответ получится таким же. если решать через т.Пифагора, приняв ВМ=х, АВ=2х