Я уже решала похожую задачу))
проблема состояла в том, что другие предложенные решения содержали тригонометрические выкладки, которые не под силу 9-класснику...
потому "родилась" идея использовать поворот (материал 9 класса)
угол АКВ -это внешний угол для треугольника DKA, значит, сумма углов KDA+KAD = 60°, это вписанные (для окружности) углы, т.е. сумма дуг, на которые опираются эти углы ∪ВА+∪CD = 120°
и мы никогда не найдем отдельные слагаемые (эти углы), т.к. данных не достаточно, потому и возникла мысль использовать именно дугу, равную сумме дуг... т.е. нужно повернуть треугольник с вершиной в центре окружности (центральным углом, соответствующим дуге АВ) с целью получить дугу в 120° (точки С и В совпадут)
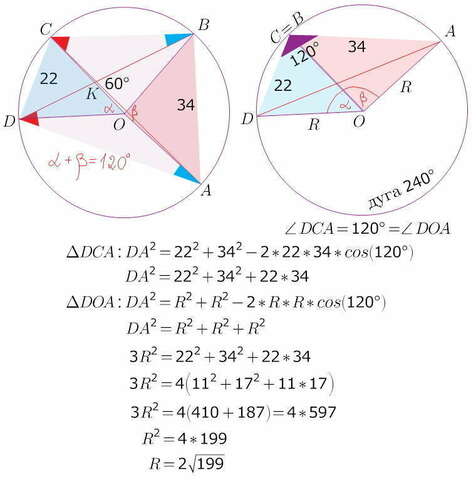
получим 4-угольник с двумя известными сторонами (22 и 34) и
двумя известными (и даже равными) углами по 120°...
остальное по теореме косинусов...