Вложение 1
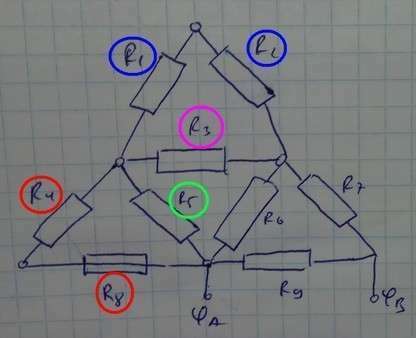
R₄ и R₈ соединены последовательно. Их эквивалентное сопротивление R₄₈=100+100=200 Ом
R₄₈ и R₅ соединены параллельно, поэтому их эквивалентное сопротивление R определяется соотношением 1/R=1/R₄₈+1/R₅;
1/R=1/200+1/100=3/200 → R=200/3
Заменяем все три рассмотренных резистора их эквивалентным сопротивлением и будем считать теперь, что R₅=200/3.
Рассуждая аналогично для последовательно включенных резисторов R₁, R₂ и параллельно включенному с ними R₃ полагаем R₃=200/3.
Вложение 2
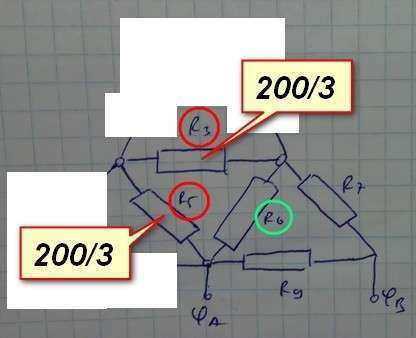
Те же рассуждения и та же формула. R₃ и R₅ включены последовательно, их эквивалентное сопротивление R₃₅=R₃+R₅=200/3+200/3=400/3.
R₃₅ включено параллельно с R₆, поэтому 1/R=1/R₃₅+1/R₆;
1/R=1/(400/3)+1/100=3/400+1/100=7/400 → R=400/7.
Заменяем все три рассмотренных резистора их эквивалентным сопротивлением и будем считать теперь, что R₆=400/7.
Вложение 3
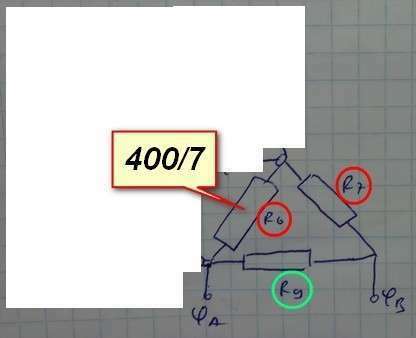
И тут ничего оригинального - все снова повторяется.
R₆ и R₇ включены последовательно, их эквивалентное сопротивление R₆₇=R₆+R₇=400/7+100=1100/7.
R₆₇ включено параллельно с R₉, поэтому 1/R=1/R₆₇+1/R₉;
1/R=1/(1100/7)+1/100=7/1100+1/100=18/1100 → R=1100/18=550/9.
Заменяем все три рассмотренных резистора их эквивалентным сопротивлением - это и будет ответ: 550/9. Перевести в десятичную дробь можно и самостоятельно.
Ответ: 550/9