Найти E(f) и D(f). С подробным решением.

Question

Дан 1 ответ

Правильный ответ

1. $y = \frac{x^2-1}{(x-10)*x-24}$
$y = \frac{x^2-1}{x^2-10x-24}$
$x^2-10x-24 \neq 0$ - единственное важное здесь условие, т.к. деление на нуль лишено смысла.
$x^2-10x-24 = 0$
$D = 100+96=14^2$
$x_{1} = \frac{10+14}{2} =12$
$x_{2} = \frac{10-14}{2} =-2$
итак,
$\left \{ {{x \neq 12} \atop {x \neq -2}} \right.$ ⇒
$D(f) = (-\infty;-2)U(-2;12)U(12;+\infty)$
$E(f) = (-\infty;+\infty )$
то есть сама функция может принимать любые значения, в том числе и значение нуль в точке х=1.

2. $y = \sqrt{ \frac{x-12}{x^2-16x+48} }$
здесь у нас ситуация посложнее.
a) $x^2-16x+48 \neq 0$ - уже проходили, на нуль не делим.
b) $\frac{x-12}{x^2-16x+48} \geq 0$ - подкоренное выражение всегда положительно или равно нулю.
разберемся сначала со знаменателем.
$x^2-16x+48=0$
$D = 64 = 8^2$
$x_{1}= \frac{16+8}{2} =12$
$x_{2} = \frac{16-8}{2} =4$
итак,
$\left \{ {{x \neq 12} \atop {x \neq 4}} \right.$
Сразу обратим внимание на то, что x=12 единственное значение икса, которое обращает числитель в нуль, но мы уже определились с тем, что $x \neq 12$ , ⇒ функция никогда не примет значение, равное нулю. А значит точка y=0 исключается из E(f).
Но, идем дальше.
$\frac{x-12}{x^2-16x+48} \ \textgreater \ 0$
(раз уж мы уже определили, что нулем это выражение не будет, то и знак сразу сделаем "строгим".
У нас возможны два случая, когда подкоренное выражение будет положительно. 1. Числитель и знаменатель одновременно положительны. 2. Числитель и знаменатель одновременно отрицательны.
$1. \left \{ {{x-12\ \textgreater \ 0} \atop {x^2-16x+48\ \textgreater \ 0}} \right.$

$2. \left \{ {{x-12\ \textless \ 0} \atop {x^2-16x+48\ \textless \ 0}} \right.$
разбираемся с первой системой:
$x-12\ \textgreater \ 0$
$x\ \textgreater \ 12$
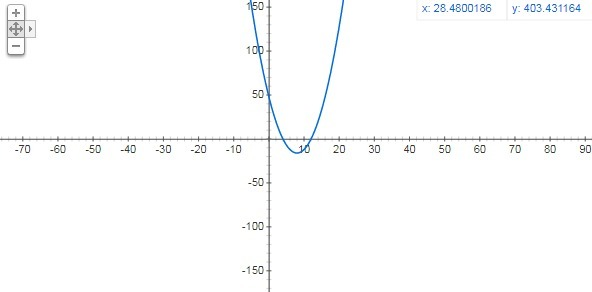
второе уравнение системы положительно на
(-∞;4)∪(12;+∞). Это мы увидим на графике (см. вложения)
⇒ решением первой системы будет x∈(12;+∞)
теперь рассмотрим вторую систему:
$x-12\ \textless \ 0$
$x\ \textless \ 12$
и x∈(4;12)
решением второй системы является: х∈(4;12)
итак,
$D(f) = (4;12) U(12;+\infty)$
$E(f) = (0;+\infty)$

Примечание: РИСУНОК, ПРЕДСТАВЛЕННЫЙ ВО ВЛОЖЕНИИ ИЛЛЮСТРИРУЕТ ПОВЕДЕНИЕ ФУНКЦИИ $y=x^2-16x+48$

drwnd_zn (15.5k баллов) 14 Май, 18