При x < 0 будет |x| = -x, тогда |x^2-2|x|-3| = |x^2+2x-3| = |(x-1)(x+3)|
При x < -3 будет (x-1)(x+3) > 0, тогда |(x-1)(x+3)| = (x-1)(x+3) = x^2+2x-3.
При x ∈ [-3; 0) будет (x-1)(x+3) < 0, тогда |(x-1)(x+3)| = -x^2-2x+3.
При x >= 0 будет |x| = x, тогда |x^2-2|x|-3| = |x^2-2x-3| = |(x+1)(x-3)|
При x ∈ [0; 3) будет (x+1)(x-3) < 0, тогда |(x+1)(x-3)| = -x^2+2x+3.
При x >= 3 будет (x+1)(x-3) > 0, тогда |(x+1)(x-3)| = x^2-2x-3.
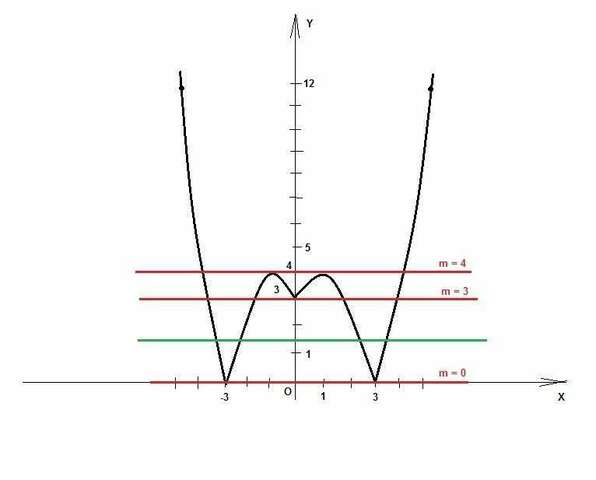
График показан на рисунке. Крайние прямые показаны красным.
4 решения будет при m = 4 и при всех m ∈ (0; 3)
При m = 3 будет 5 решений, при m = 0 будет 2 решения.
Одна прямая из промежутка (0; 3) показана зеленым, это 4 решения.
Ответ: m ∈ (0; 3) U [4]