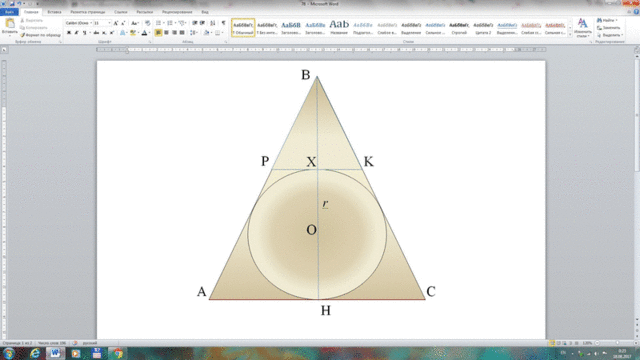
R⊥PK, r⊥AC - по свойству касательной, тогда PK║AC, значит ∠BРK=∠А, ∠BKP=∠C - как соответственные, а, поскольку ∠А=∠С - по свойству равнобедренного треугольника, то ∠ВРК=∠ВКР и ΔРВК∼ΔАВС - по двум углам.
Пусть ВН - биссиктриса, медиана и высота по свойству равнобедренного треугольника и ВН∩РК=Х, тогда О∈ВН и О - ортоцентр. Значит 3ВХ=ВН=3r - по свойству медианы.
Таким образом, РК/АС=РВ/АВ=1/3 ⇒ РК=12/3=4 (см)
Поскольку в ΔРВК РВ=ВК - по свойству равнобедренного треугольника, то РВ=(Р-РК)/2=(8-4)/2=2(см) ⇒ АВ=ВС=3РВ=3*2=6(см)