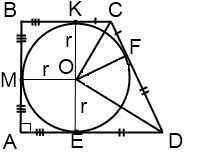
1) Пусть ABCD - прямоугольная трапеция, в которую вписана окружность. CF=4 см и FD=25 см.
2) Площадь трапеции можно найти по формуле:
S=(AD+BC)*AB/2, где AD и BC - основания трапеции, AB - высота трапеции.
3) Можно использовать следующее свойство для прямоугольной трапеции, в которую вписана окружность:
Если точка касания делит боковую сторону на отрезки m и n, то радиус вписанной окружности равен r=√(mn).
Находим радиус вписанной окружности:
r=√(4*25)=√100=10 (см).
Значит, высота АВ=2r=2*10=20 (см).
4) Так как центр вписанной окружности является точкой пересечения биссектрис углов трапеции, то KC=CF=4 см, FD=DE=25 см.
5) AMOE=MBKO - квадраты со стороной, равной радиусу вписанной окружности, т.е. AE=BK=10 см.
Таким образом, получаем, AD=10+25=35 (см), BC=10+4=14 (см).
6) Находим площадь трапеции:
S=(AD+BC)*AB/2=(35+14)*20/2=49*10=490 (cм²).
Еще площадь прямоугольной трапеции, в которую вписана окружность можно найти по отдельной формуле:
S=AD*BC (произведение оснований).
S=35*14=490 (см²).
Ответ: 490 см².