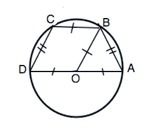
В окружность можно вписать четырехугольник тогда и только тогда, когда сумма его противоположных углов равна 180°.
Следовательно, вписанной может быть только равнобедренная трапеция - сумма ее противоположных углов равна 180°.
Проведем радиус ОВ. По условию АD=2 CB. ⇒
DO=CB=AO.
В четырехугольнике ВОDC стороны DO и ВС параллельны и равны. ⇒ Четырехугольник BODC - параллелограмм, и DC=BO=DO=R,
АО=ОВ=R. AB=CD=R
Следовательно, ∆ АОВ - равносторонний, все его углы равны 60°.
В равнобедренной трапеции углы при основаниях равны.
∠D=∠A=60°, ∠С=∠В=180°-60°=120°