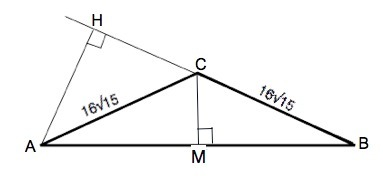
Данный по условию синус угла ВАС=0,25, ⇒ угол ВАС меньше 30°, чей синус равен 0,5, поэтому
∆ АСВ - тупоугольный. Высота АН будет проведена к продолжению ВС.
Опустим высоту СM на АВ.
АВ= 2 АM
B треугольникe САM катет АM=АС•cos∠BAC.
Найдем cos∠BAC из основного тригонометрического тождества:

cos∠BAC=√(1-sin²∠BAC)=√(1-1/16)=
АМ=
 =60
=60
AВ=2•60=120
∆ ACB - равнобедренный, углы А и С равны. ⇒ равны их синусы.
АН=АВ•sin НВА
АН=120•0,25=30 (ед. длины)