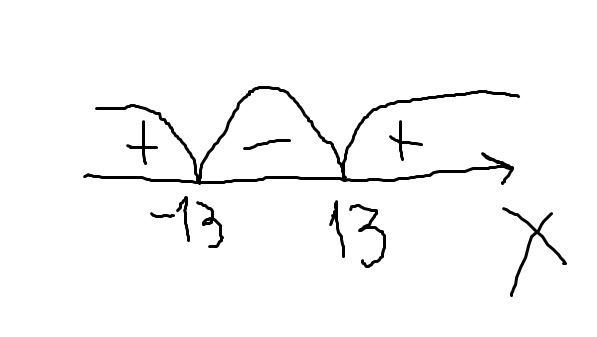Стоп-стоп-стоп, давайте по порядку :)
Найдем точки максимума.
Для этого найдем производную функции и затем нули производной от этой функции.
Скорее всего, вы подразумевали функцию такого вида (на будущее: ставьте скобки):

Объяснять, как находить производную, не буду, т.к. у вас другая проблема:

Приравняем к нулю и заметим, что корни 13 и -13.
Используем метод интервалов(фото).
знак плюса- тот промежуток, где f'(x) >0 , а знак минуса - f'(x) <0.<br>Точка максимума, это тот x, при котором плюс уходит в минус.
x = -13 - ваша точка максимума.
В чем была ваша проблема? :)