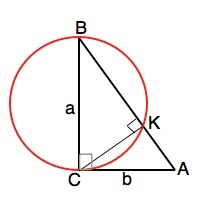
Дан прямоугольный треугольник АВС (угол С=90°). В этом треугольнике провели окружность так, что катет ВС-диаметр этой окружности. К-точка пересечения этой окружности и гипотенузы. Найти длину отрезка СК, если ВС=а, АС=b
Так как ВС - диаметр, а К - точка на окружности, то угол СКВ, опирающийся на диаметр,- прямой, и СК - высота ∆ АВС.
Воспользуемся формулой площади прямоугольного треугольника.
S=BC•AB:2
S=a•b:2
Площадь можно найти и по формуле
S=a•h:2, где а - гипотенуза, h- высота. проведенная к ней. ⇒
h=2S:AB
AB=√(BC²+AC²)=√(a²+b²)
h=ab:√(a²+b²)