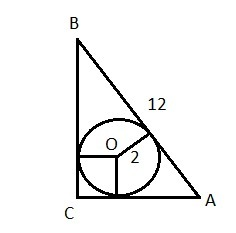
Пусть ΔАВС - прямоугольный, ∠С=90°, АВ=12 см, r=2 cм.
Радиус вписанной окружности в прямоугольный треугольник можно найти по формуле:
r=p-c, где р - полупериметр треугольника, с - гипотенуза.
р=r+c=2+12=14 (см).
Значит периметр Р=2р=2*14=28 (см).
Ответ: 28 см.