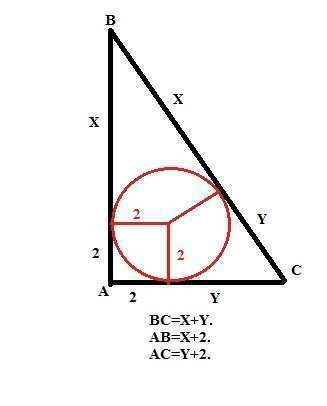
В прямоугольном треугольнике точки касания вписанной окружности со сторонами треугольника делят эти стороны на пары РАВНЫХ касательных, проведенных из одной точки (вершины треугольника) к этой окружности. Кроме того, эти точки отделяют на катетах, считая от вершины прямого угла, отрезки, равные радиусу вписанной окружности.
Тогда можно записать, что
X+Y=10 и по Пифагору (X+2)²+(Y+2)²=100. Решаем эту систему методом подстановки: Y=10-X.
X²+4x+4+(10-X)²+4(10-X)+4=100.
Отсюда X²-10X+24=0.
X1=6, Y1=4.
X2=4, Y2=6.
то есть катеты нашего треугольника равны 6см и 8см.
Тогда S=(1/2)*6*8=24см² Р=6+8+10=24см. это ответ.