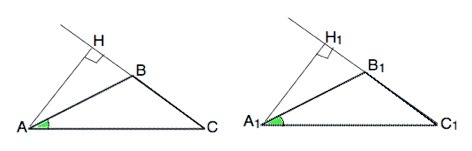
Так как по условию треугольники равны, то равны все их сходственные элементы. ⇒
∠С=∠С1, АС=А1С1.
Расстояние от точки до прямой - длина отрезка, проведенного перпендикулярно к ней, Для данных треугольников эти расстояния – высоты АН и А1Н1 треугольников соответственно.
∠В и ∠В1 тупые, поэтому АН и АН1 пересекут прямые СВ и СВ1 вне треугольников.
Рассмотрим ∆ АНС и Δ А1Н1С1. Они прямоугольные, гипотенузы АС=А1С1, ∠С=∠С1. Треугольники равны по гипотенузе и острому углу. Следовательно, АН=А1Н1.
Т.е.расстояния от вершин А и А1 соответсвенно до прямых ВС и В1С1 равны, что и требовалось доказать.