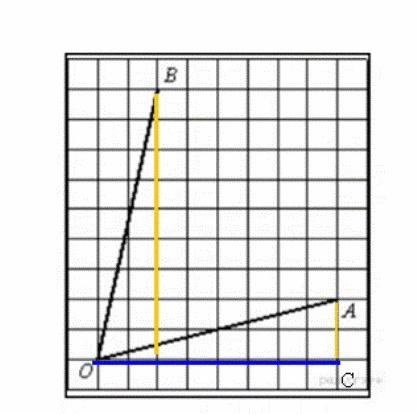
Тангенс - это отношение противолежащего катета к прилежащему катету. Но это в прямоугольном треугольнике! Поэтому с помощью дополнительных построений получим два прямоугольных треугольника,а в них найдём тангенсы ∡АОС и ∡ВОС.
tg<АОС=2/8=1/4=0,25, (где 2 клетки и 8 клеток - катеты)</p>
tg<ВОС=9/2 = 4,5</p>
А теперь очевидно, что:
tg<АОВ = tg(<ВОС - <АОС)</p>
Используем формулу тангенс разности:

tg<АОВ = (tg<ВОС - tg<АОС)/(1+tg<ВОС*tg<АОС)</p>
tg<АОВ = (4,5 - 0,25)/(1+ 4,5*0,25)=</p>
=4,25/2,125=2
Ответ: tg<АОВ = 2</p>