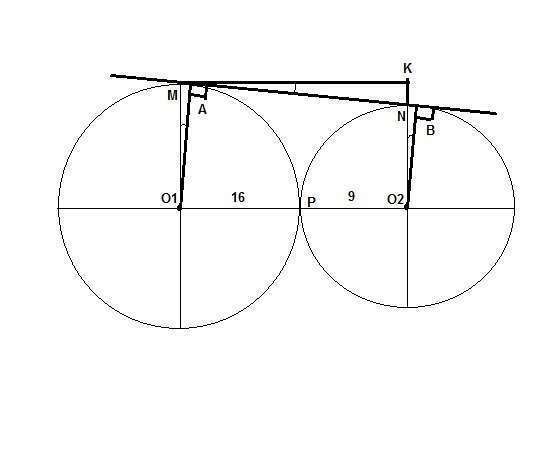
Эти окружности касаются друг друга внешним образом.
16 + 9 = 25.
Радиусы O1A || O2B (O1A и O2B оба перпендикулярны к AB).
Нарисуем треугольник MNK, где MK || O1O2, |MK| = |O1O2| = 25.
M и N - кончы вертикальных радиусов в окружностях.
|O1M| = 16; |O2N| = 9; |O2K| = |O1M| = 16; |KN| = 16 - 9 = 7.
tg (KMN) = KN/MK = 7/25
Углы наклона радиусов O1A и O2B равны углу KMN
tg (MO1A) = tg (KMN) = 7/25 = MA/O1M = MA/16
MA = 16*7/25 = 112/25
tg (KO2B) = tg (KMN) = 7/25 = NB/O2N = NB/9
NB = 9*7/25 = 63/25
По теореме Пифагора
MN^2 = MK^2 + KN^2 = 25^2 + 7^2 = 625 + 49 = 674
MN = √674
AB = MN - MA - NB = √674 - 112/25 - 63/25 = √674 - 175/25 = √674 - 7