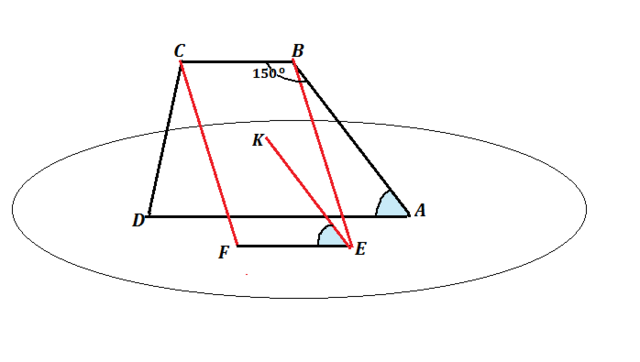
Основание АD трапеции ABCD лежит в плоскости α .Через точки B и C проведены параллельные прямые , пересекающие плоскость α в точках E и F соответственно. а) каково взаимное расположение прямых EF и AB?
б) Чему равен угол между прямыми EF и AB, если ABC = 150°?
_____________
а) АД лежит в плоскости альфа. ВС параллельна АD, след, ВС параллельна плоскости α.
По условию CF|| BE.
Отрезки параллельных прямых, заключенные между плоскостью и параллельной ей прямой, равны. ВЕ параллельна и равна СF. Следовательно, СВЕF параллелограмм, ⇒ ЕF равна и параллельна ВС Две прямые, параллельные третьей прямой, параллельны между собой.
АD|| ВС, ЕF || ВС след ЕF || АD.
ЕF лежит в плоскости α, ВА пересекает ее в точке, не принадлежащей ЕF. Если одна из двух прямых лежит в плоскости, а другая пересекает эту плоскость в точке, не принадлежащей первой прямой, то эти прямые скрещиваются.⇒
прямые EF и AB - скрещивающиеся.
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными данным.
. Сумма углов при боковой стороне трапеции 180°.
Угол ВАD=180º-150º=30°
Проведем в плоскости ВЕF прямую ЕК, параллельную АВ.
Т.к. ЕF|| АD, а ЕК || АВ,
угол KEF=углу ВАD и равен 30°
-------------
Если ВЕ и СF проведены в плоскости трапеции АВСD, ЕF будет лежать на АD и в этом случае EF и АВ лежат в одной плоскости и не параллельны. В этом случае АВ и EF пересекаются, и угол между ними равен 30º