5(3)
Y = -x² + 4x + 1 - функция
Y' = - 2x + 4 = - 2*(x - 2) - первая производная
Локальные экстремумы - в корнях первой производной.
Возрастает - Х∈(-∞;2]
Х1 = 2 - точка максимума - Ymax(2) = 5.
Убывает - Х∈[2;+∞)
6(2)
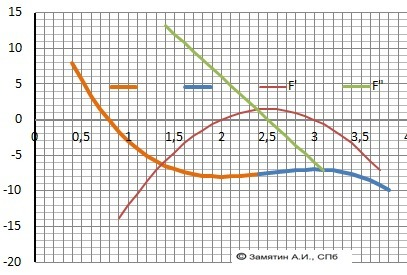
Y = -2x³ + 15x² -36x + 20 - функция
Y = - 6x² + 30х - 36 - первая производная
Находим корни квадратного уравнения
Y = - x² + 5x - 6 ( сократили на 6)
. D=36. x1= 2, x2 = 3
Убывает - Х∈(-∞;2]∪[3;+∞)
Минимум - X=2. Ymin(2) = -8
Возрастает - X∈[2;3]
Максимум - Х=3 Ymax(3) = -7
График прилагается.
7(1)
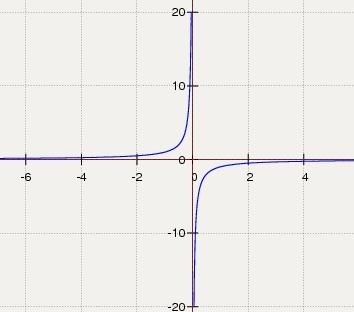
Y = - 1/x - функция
Область определения - Х≠0
Y' = 1/x² - первая производная
Возрастает - Х∈(-∞;0)∪(0;+∞)
График прилагается.