Две вершины вписанного в полукруг квадрата лежат на диаметре, а две других - на полуокружности - как половина вписанного в круг прямоугольника, стороны которого лежат на равном расстоянии от центра окружности по разные стороны от диаметра.
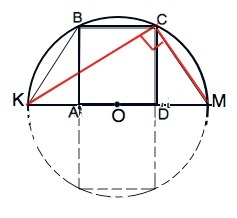
Пусть данный квадрат будет АВСD, вершины А и D лежат на диаметре КМ, В и С - на полуокружности. .
ВС||KM, ⇒КВСМ - трапеция , причем равнобедренная ( в окружность можно вписать только равнобедренную трапецию.
Высота равнобедренной трапеции делит большее основание на отрезки, больший из которых равен полусумме оснований, меньший - их полуразности. ⇒
КD=(2r+BC):2, DМ=(2r-ВС):2
∆ КСМ - прямоугольный (угол С опирается на диаметр)
Высота прямоугольного треугольника, проведенная из прямого угла, есть среднее пропорциональное отрезков, на которые она делит гипотенузу.
Примем сторону квадрата равной а. Его площадь будет равна а²
a²= [(2r+a):2]•[(2r-a)²2] ⇒
a²=(4r²-a²):4
4a²=4r²-a²
5a²=4r²
a²=4r²/5 - это площадь квадрата.