ДАНО
Y= 2x³-3x²-12x-1
ИССЛЕДОВАНИЕ
1. Область определения - Х∈(-∞;+∞) - непрерывная.
2. Пересечение с осью Х
Y(x)=0 при x1 = -1.7555, x2 = - 0.08525, [3 = 3.34
3. Пересечение с осью У Y(0)= -1.
4. Проверка на четность.
Y(-x) = - 2x³ -3*x² + 12x - 1 ≠ Y(x) - функция ни чётная ни нечётная.
5. Первая производная
Y'(x) = 6x² - 6x - 12 - график парабола
6. Монотонность - корни производной - x1 = -1 x2 = 2
Возрастает - Х∈(-∞;-1]∪[2;+∞)
Ymax(-1) = 6
Убывает - X∈[-1;2]
Ymin(2) = - 21.
7. Вторая производная
Y"(x) = 12x - 6 - график - прямая
8. Точка перегиба
Y"(x)=0 при Х = 0,5 и Y(0.5) = -7.5
9. Выпуклая - "горка" - X∈(-∞;0.5]
Вогнутая - "ложка" - X∈[0.5;+∞)
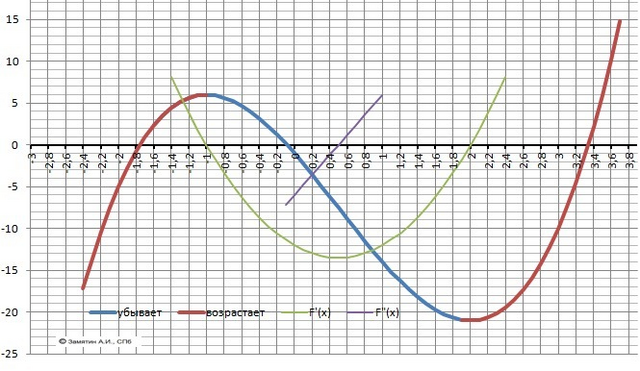
10. График прилагается.