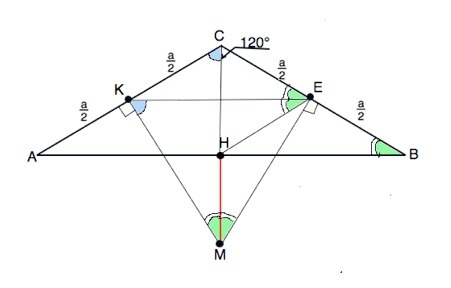
Расстояние от точки до прямой - длина перпендикулярного отрезка.
В равнобедренном о АСВ углы при А и В равны (180°-120°):2=30°
К и Е - середины АС и ВС соответственно.
След. АК=КС=СЕ=ВЕ=а/2
КЕ║АВ по свойству средней линии.
∠СКЕ=∠СЕК=30° (соответственные углам А и В при пересечении параллельных КЕ и АВ секущими).
В четырехугольнике СКМЕ углы при К и Е равны 90° ( МК и МЕ - перпендикуляры)
. Сумма углов четырехугольника 360°. ⇒ ∠КМЕ=360°-2•90°=60°.
∠ЕКМ=∠КЕМ=90°-30°=60°
∆ МЕК- равносторонний.
Срединные перпендикуляры треугольника пересекаются в одной точке. ⇒ СМ - срединный перпендикуляр, Н - середина АВ, и АН=ВН, ⇒
СН - медиана и биссектриса ∆ АСВ. ∠НСВ=60°
СН противолежит углу 30° ⇒ СН=СВ:2=а/2
СЕ=а/2, СН=а/2 ⇒∆ НСЕ- равносторонний, НЕ=а/2.
∠СМЕ=∠МЕН=30°
∆ МНЕ - равнобедренный. ⇒ МН⊥АВ, МН=ЕН=а/2.
* * *
Или как вариант:
∆ АСВ - равнобедренный. К и Е - середины АС и ВС соответственно.
СЕ=а/2
Срединные перпендикуляры треугольника пересекаются в одной точке. ⇒ СМ - срединный перпендикуляр к АВ.
СН ⊥AB - высота и биссектриса, ∠НСВ=60°
∆ НСВ прямоугольный, СН=ВС•cos60°=a•1/2=a/2
CЕ=СН, угол НСЕ=60°, ⇒∆ НСЕ равносторонний и НЕ=СЕ=а/2
В ∆ СМЕ угол СМЕ=90°-60°=30°
В ∆ МНЕ ∠МЕН =∠СЕМ-∠СЕН=90°-60°=30°
∆ МНЕ - равнобедренный, ⇒
МН=НЕ=а/2