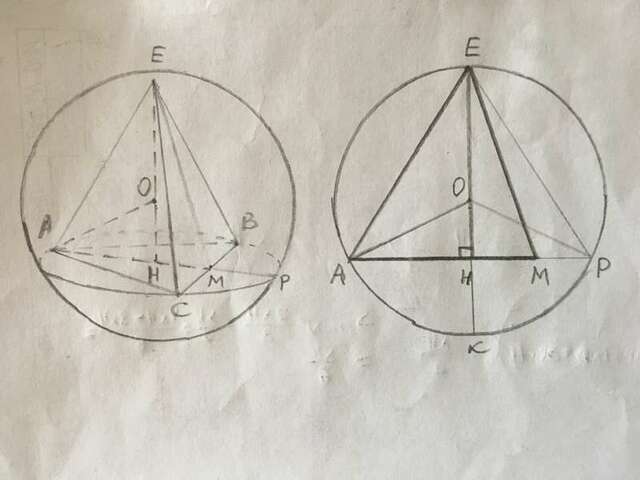
В правильной пирамиде ЕАВС ЕА=ЕВ=ЕС=b, ЕН=h.
Так как боковые рёбра пирамиды равны, то основание высоты ВН точка Н лежит в центре описанной около основания окружности.
Рассмотрим сечение пирамиды, проходящее через высоту пирамиды ЕН и высоту основания АМ.
Диаметр ЕК перпендикулярен хорде АР, значит АН=РН.
Прямоугольные треугольники ЕАН и EPH равны по двум катетам, значит ЕА=ЕР.
В треугольнике ЕАН sinA=ЕН/ЕА=h/b.
В равнобедренном треугольнике АЕР АО=ЕО=РО=R - радиус описанной окружности, совпадает с радиусом шара.
По теореме синусов R=EP/2sinA=b/(2h/b)=b²/2h.
Объём шара: V=4πR³/3,
V=4πb⁶/(24h³)=πb⁶/(6h³) - это ответ.