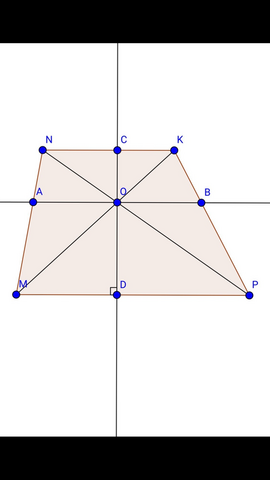
Треугольники МОР и KON подобны (свойство трапеции), значит СО:ОД=NK:MP=24:40=3:5.
В треугольнике МКР ОВ║МР, значит ΔМКР~ΔОКВ. КВ:ВР=СО:ОД=3:5 ⇒ КВ:КР=3:8.
ОВ:МР=КВ:КР ⇒ ОВ=КР·МР/КВ=3·40/8=15 см.
Аналогично треугольники МNР и ANO подобны.
AO:MP=NA:NM=КВ:КР, значит АО=ОВ=15 см, следовательно АВ=30 см - это ответ.