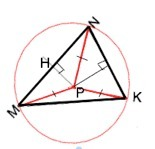
Точка пересечения серединных перпендикуляров треугольника является центром описанной окружности.
Поэтому РК=РN=PM=R
По т.синусов


R=10√3:2=5√3
PK=5√3
* * *
Если т.синусов Вам еще не знакома, можно найти R из ∆ MPH по т.Пифагора, т.к. ∠РМN=∠PNM=(180°-120°):2=30°