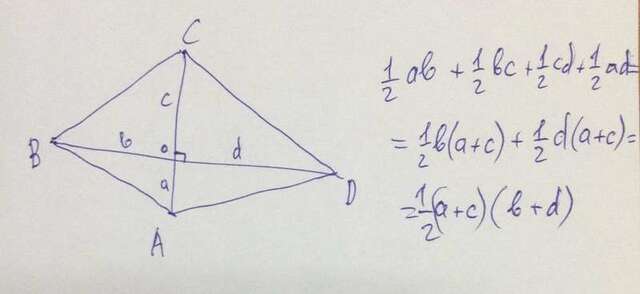Построим такой четырёхугольник ABCD. Его площадь равна сумме площадей составляющих его прямоугольных треугольников AOB, BOC, COD и DOA. Площадь прямоугольного треугольника равна половине произведения его катетов. Обозначим отрезки, являющиеся катетами этих треугольников как a, b, c и d. Ну и путём нехитрых вычислений получаем нужный результат =)