Задача а)
ДАНО Y = 2x - 3
Решение
1. Область определения - Х∈(-∞;+∞) или X∈R - непрерывная функция - прямая.
2. Пересечение с осью Х
0 = 2х - 3 и х= 1,5
3. Пересечение с осью У
У(0) = -3
4) Проверка на четность.
у(-х) = - 2х -3 ≠ у(х) - функция ни чётная ни нечётная.
5. Первая производная
Y'(x) = 2 - нет максимумов и минимумов.
6. Монотонность функции.
Возрастает - Х∈(-∞;+∞)
Минимум - У(-1) = -6
Максимум - У(4) = 2*4 - 3 = 5
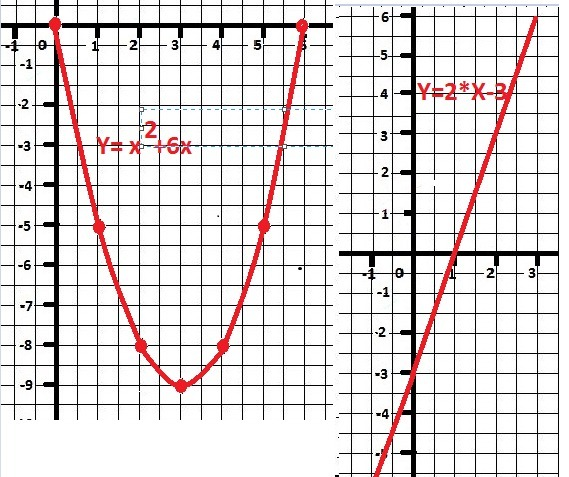
7. График прилагается.
Задача б)
ДАНО
Y = x² +6x = x*(x+6)
1 Область определения - Х∈(-∞;+∞) - непрерывная.
2. Пересечение с осью Х
Х1 = 0 и Х2 = - 6.
3. Пересечение с осью У - Y(0) = 0.
4. На чётность
Y(-x) = x² -6x ≠ Y(x) - функция ни чётная ни нечётная.
5. Первая производная.
Y'(x) = 2x-6 = 2*(x-3)
6. Поиск экстремумов.
Y'(x) = 0, X = 3
7. Локальный минимум - У(3) = -9.
8. Графики в приложении.