5.
ДАНО
Исследовать на монотонность функцию
Y = x³ + 3x² - 9x
ИССЛЕДОВАНИЕ
1. Первая производная функции.
Y'(x) = 3x² + 6x - 9.
F(x)= x²+2x-3
2 Точки экстремума в корнях первой производной.
F(x) = 0 - решаем квадратное уравнение и получаем корни.
x1 = -3 и х2 = 1
3. Возрастает - Х∈(-∞;-3]∪[1;+∞)
Локальный максимум - Y(-3) =
Убывает - Х∈(-3;1]
Локальный минимум - Y*(1) = -4
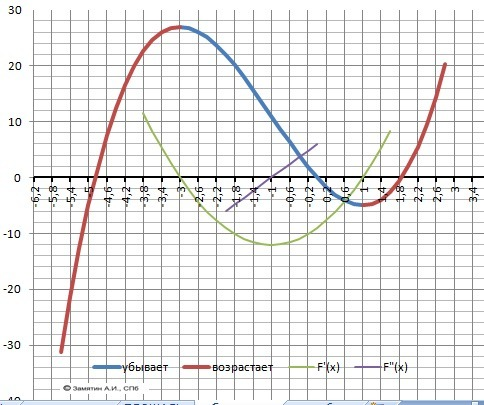
4. График функции - в приложении.