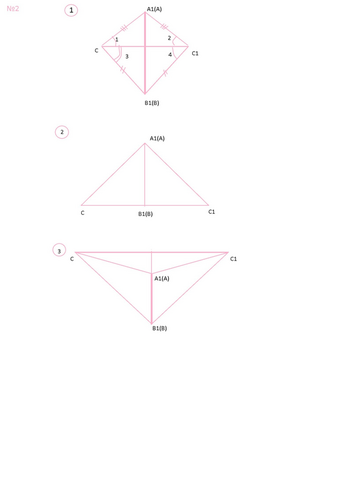
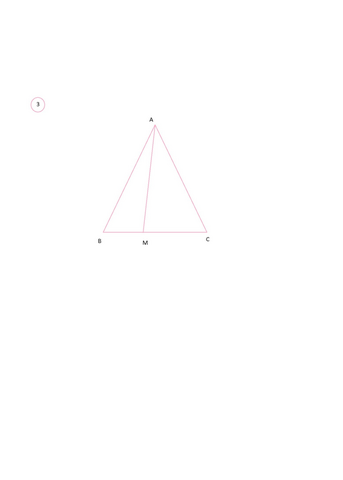2. Рассмотрим треугольники авс и а1в1с1, у которых стороны одного треугольника равны сторонам другого треугольника.
Докажем равенство:
Приложим треугольник авс к треугольнику а1в1с1 так, чтобы вершина а совместилась с вершиной а1, в с в1, а с и с1 оказались по разные стороны от прямой а1в1.
Возможны три случая: луч с1с проходит внутри угла а1с1в1; луч с1с совпадает с одной из сторон этого угла; луч с1с проходит вне угла а1с1в1.
Рассмотрим 1 случай: Так как по условию теоремы стороны ас и а1с1, вс и в1с1 равны, то треугольники а1с1с и в1с1с-равнобедренные. По теореме о свойстве углов р/б треугольника угол 1=углу 2, угол 3=углу 4, поэтому угол а1св1=углу а1с1в1. Из этого следует что ас=а1с1, вс=в1с1, угол с=углу с1.
Следовательно треугольники равны по первому признаку. Теорема доказана.
3. А вот в 3 задаче наверное где-то ошибка, если М лежит на основании вс, то углы МСВ и МВС не существуют.