В остроугольном треугольнике ABC ** сторонах АС и ВC отмечены соответственные точки N и L...

Question

В остроугольном треугольнике ABC на сторонах АС и ВC отмечены соответственные точки N и L так, что NL параллельна AB и NL=LB; На стороне AB отмечена точка M так, что что угол LMB = углу ACB. Найдите CN, если LM=5 С чертежом, пожалуйста.

Answer 1

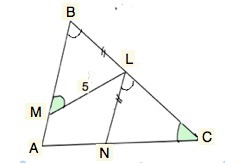
Сделаем рисунок. 

По условию ВL=LN, 

LN||AC

Рассмотрим ∆ BML и  ∆ CNL

Углы ВМL = NCL ( т.к. он равен АСВ)

углы МВL=NLC - равные соответственные при пересечении параллельных  LN||AC секущей ВС.

∆ BML  подобен ∆CNL по двум равным углам. 

Следовательно, их третьи углы тоже равны. 

Тогда эти треугольники не только подобны, но и равны, так как имеют по равной стороне ВL=LN  и прилежащим к ней углам. 

Значит, CN равна ML и равна 5 

---