Числа 11 и 3 можно отбросить (на множество решений это не влияет)

Дробь принимает отрицательные значения если числитель и знаменатель имеют разные знаки.
Для решения такого неравенства удобно использовать метод интервалов.
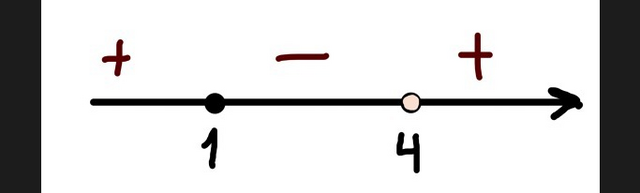
Для этого отметим на числовой прямой нули числителя и знаменателя, числа 1 и 4 .
Но точку 4 необходимо выколоть, тк при х=4 знаменатель равен нулю, а х=1 входит в множество решений неравенства тк неравенство не строгое.
Теперь необходимо найти промежутки знаков постоянства.
Для чисел (4; +∞) дробь принимает положительные значения. (проверьте это для любого числа из этого множества)
Для чисел (1;4) дробь принимает отрицательные значения
Для чисел (-∞;1)
дробь больше нуля.
Ответ :

∈ [1;2) U (2;4)