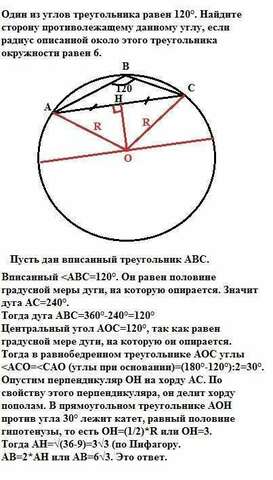
Пусть дан вписанный треугольник АВС.
Вписанный Центральный угол АОС=120°, так как равен градусной мере дуги, на которую он опирается.
Тогда в равнобедренном треугольнике АОС углы <АСО=<CAO (углы при основании)=(180°-120°):2=30°.<br>Опустим перпендикуляр ОН на хорду АС. По свойству этого перпендикуляра, он делит хорду пополам. В прямоугольном треугольнике АОН против угла 30° лежит катет, равный половине гипотенузы, то есть ОН=(1/2)*R или ОН=3.
Тогда АН=√(36-9)=3√3 (по Пифагору).
АВ=2*АН или АВ=6√3. Это ответ.