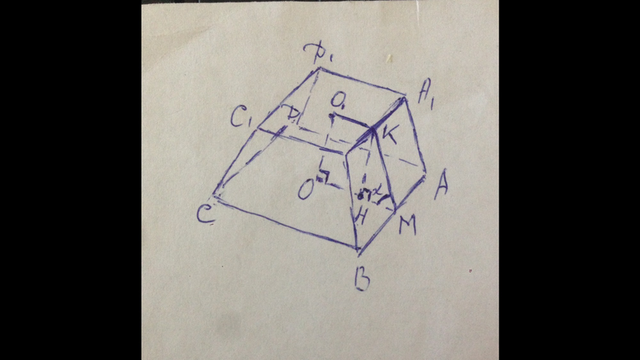
В основаниях пирамиды лежат квадраты.
Пусть АВ=а, А1В1=b, тогда а=3/√2=3√2/2 см и b=1/√2=√2/2 см.
О1К⊥А1В1 и КМ⊥А1В1, значит ∠О1КМ=120°. О1К║ОМ ⇒ ∠КМО=180-120=60°.
ОМ=а/2=3√2/4 см, О1К=b/2=√2/4 см.
КН⊥ОМ. МН=ОМ-ОН=ОМ-О1К=3√2/4-√2/4=√2/2 см.
В прямоугольном тр-ке КМН КМ=МН/cos60=√2 cм.
Площадь боковой поверхности состоит из четырёх равных трапеций, представляющих боковые грани пирамиды, значит площадь можно записать следующим образом:
Sб=4h(a+b)/2=2h(a+b), где h - высота боковой грани. h=КМ.
Sб=2√2(3√2/2+√2/2)=(2√2)²=8 см² - это ответ.