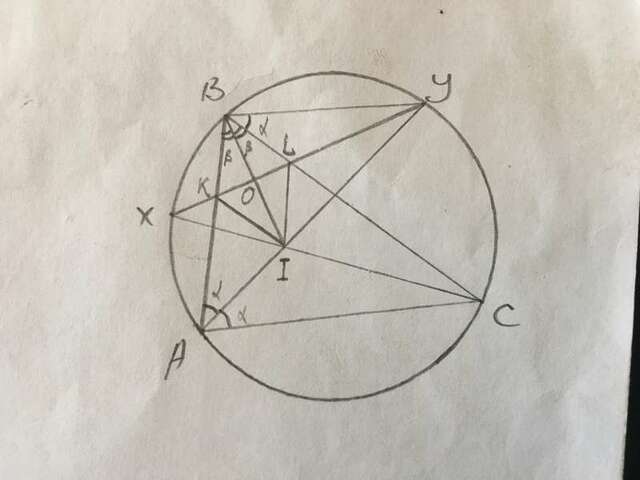
Для доказательства используем теорему о трилистнике, которая гласит, что если биссектриса угла А треугольника АВС пересекает окружность в точке Y и точка I - центр вписанной в ΔАВС окружности, то YB=YI=YC.
Обозначим углы ВАI и САI как α, а углы АВI и СВI как β.
Вписанные углы YAС и YBС равны α т.к. опираются на одну дугу.
∠BIY - внешний треугольника АВI, значит ∠BIY=∠ВAI+∠АВI=α+β.
В треугольнике ВYI ∠YВI=∠BIY=α+β, значит он равнобедренный. YB=YI.
∠ВYX=∠AYX так как они опираются на равные дуги ВХ и АХ, значит YX - биссектриса равнобедренного тр-ка ВYI, значит YX⊥BI и BO=OI.
Треугольники КВО и LBO равны так как ВО - общая сторона и прилежащие к ней углы β и 90° равны, значит КО=ОL.
В четырёхугольнике ВKIL диагонали пересекаются под прямым углом и точкой пересечения делятся пополам, значит ВKIL - ромб.
Доказано.