Две концентрические окружности имеют общий центр О. Из произвольной точки А окружности...

Question

Две концентрические окружности имеют общий центр О. Из произвольной точки А окружности большего радиуса проведены две касательные AF и AK к меньшей,которые пересекают большую окружность в точках D и E соответственно,, угол DAE=60 градусов. Найдите радиус меньшей окружности, если радиус большей равен 8 см

Answer 1

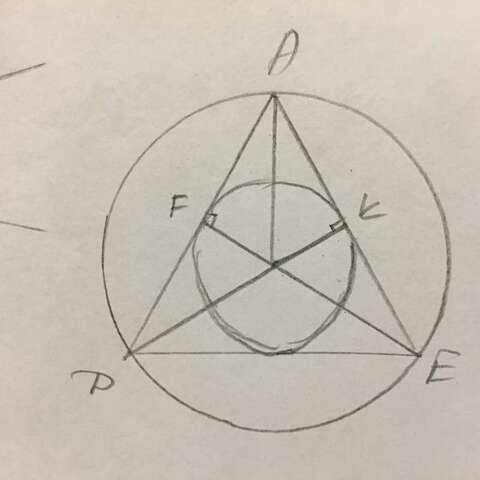
АF=AK как касательные, проведённые из одной точки. OF=OK=R.
Треугольники AFO и АКО равны по трём сторонам.
Равнобедренные треугольники АОД и AOE равны т.к. ОД=ОЕ, АО - общая сторона, OF=OK ⇒ АК=КЕ и AF=FD ⇒ АЕ=АД.
Треугольник АЕД равнобедренный, значит ∠АДЕ=∠АЕД=(180-60)/2=60°.
Треугольник АЕД правильный, данные окружности имеют общий центр, бОльшая окружность - описанная, меньшая касается сторон АД и АЕ, значит она вписанная. 
r=R/2=8/2=4 см - это ответ.

---

Comments

Спасибо огромное. Вы мне ооочень поомоглии)