Решите неравенствоsqrt(2x^2-18x+16)+4<x

$\sqrt{2x^2-18x+16}+4<x$

\sqrt{2x^2-18x+16}" alt="x-4>\sqrt{2x^2-18x+16}" align="absmiddle" class="latex-formula">

2x^2-18x+16; x-4>0" alt="2x^2-18x+16 \geq 0; (x-4)^2>2x^2-18x+16; x-4>0" align="absmiddle" class="latex-formula">

решаем первое неравенство
$2x^2-18x+16 \geq 0$
$x^2-9x+8 \geq 0$
$(x-1)(x-8) \geq 0$
нули функции х-1=0, х=1
х-8=0, х=8
коэффициент при x^2 равен 1(ветви параболы верх), значит решение
х є $(-\infty; 1] \cup [8;+\infty)$

решаем второе

2x^2-18x+16" alt="x^2-8x+16>2x^2-18x+16" align="absmiddle" class="latex-formula">
$x^2-10x<0$
$x(x-10)<0$
нули функции х=0,
х-10=0, х=10
коэффициент при x^2 равен 1 (ветви параболы верх) ,значит решение
х є (0;10)

0" alt="x-4>0" align="absmiddle" class="latex-formula">

4" alt="x>4" align="absmiddle" class="latex-formula">
обьдиняя находим решение
x є $[8;10)$

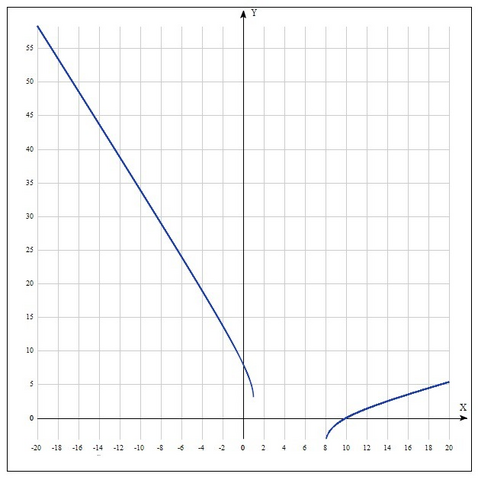
во вложении граффик $y=\sqrt{2x^2-18x+16}+4-x$
по граффику видно что л.ч. отрицательная при x є $[8;10)$