Сначала найдём производные. Потом найдём промежутки монотонности (возрастания и убывания), затем отметим точки минимума и точки максимума (экстремумы).
Там, где производная больше нуля, функция возрастает, где меньше - убывает. Точка, где возрастание меняется на убывание - точки максимума, убывание на возрастание - минимума.


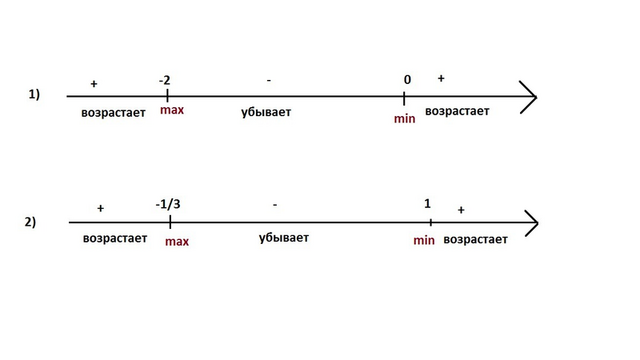
Ответ: 1) функция возрастает на (-∞; -2] и на [0; +∞), убывает на [-2; 0].
x = -2 - точка максимума, x = 0 - точки минимума;
2) функция возрастает на (-∞; -1/3] и на [1; +∞), убывает на [-1/3 1].
x = -1/3 - точка максимума, x = 1 - точки минимума.