Преобразуем суммы в произведения по формулам:
sin x + sin y = 2 sin (x + y)/2 cos (x - y)/2
cos x + cos y = 2 cos (x + y)/2 cos (x - y)/2
Тогда левая часть уравнения превратится в такую:
2 sin 2x cos x / (2 cos 2x cos x) = sin 2x / cos 2x
Раскладываем синус двойного аргумента и окончательно в левой части будем иметь
2 sin x cos x / cos 2x
2 sin x cos x / cos 2x = 2 cos x / sin 3x
2cos x * (sin x / cos 2x - 1 / sin 3x) = 0
На cos x мы сокращали дробь, поэтому этот косинус не равен нулю. Значит,
sin x / cos 2x - 1 / sin 3x = 0
sin x sin 3x - cos 2x = 0
Раскладываем произведение синусов в сумму (sin x sin y = 1/2 (cos(x - y) - cos (x + y)), а потом полученное опять в произведение:
sin x sin 3x - cos 2x = 0.5cos 2x - 0.5cos 4x - cos 2x = -0.5(cos 4x + cos 2x) = -cos 3x cos x = 0
Опять делим на cos x, е равный нулю, и впервые получаем уравнение, похожее на решаемое:
cos 3x = 0
3x = pi/2 + pi n
x = pi/6 + pi/3 n
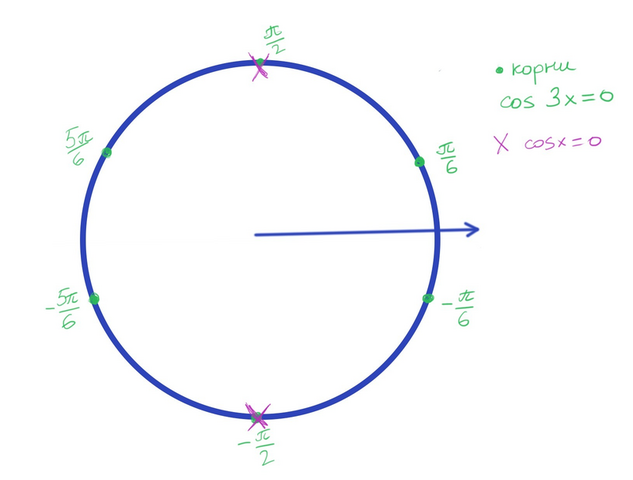
Осталось отобрать те корни, которые случайно не обнуляют какие-нибудь знаменатели. Я это делаю при помощи тригонометрической окружности.
Ответ. +-pi/6 + pi n, n целое