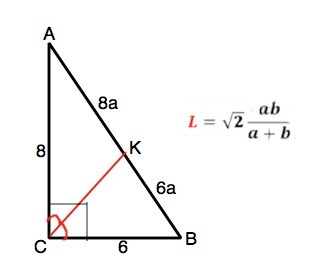
Обозначим биссектрису СК. Одно из свойств биссектрисы: отношение отрезков, на которые биссектриса делит сторону, противоположную углу, из которого проведена, равно отношению сторон, содержащих этот угол.
АК:ВК=АС:ВС
Пусть коэффициент этого отношения а.
Тогда АК=8а, ВК=6а
Отношение ВС:АС =3:4 - отношение катетов египетского треугольника, поэтому гипотенуза АВ=10 см
АВ по т.Пифагора АВ также найдем равной 10 см.
а=АВ:(8+6)=5/7 Отсюда
АК=8•4/7=40/7
sin A=BC:AB=6:10=0,6
По т.синусов
СК/sin∠CAK=AK/sin∠ACK
CK:0,6=40/7):√2/2
CK=48:7√2=24√2):7= ≈4,849 см
-------------
Примечание: для биссектрисы треугольника есть формула. В частности, для прямоугольного треугольника нахождение биссектрисы через катеты она дана в приложении с рисунком.