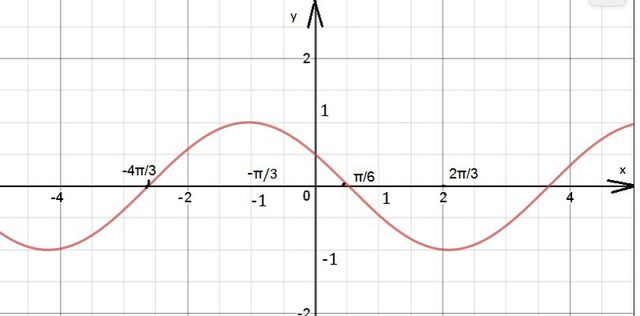
А) см. рисунок в приложении
График получен из графика у=соsx сдвигом на (π/3) влево.
б) у=соsx возрастает на (-π+2πk;2πk), k∈Z
Решаем неравенство:
-π+2πk ≤ x+(π/3)≤2πk, k∈Z
у=сos(x+(π/3)) возрастает при
(-4π/3)+2πk ≤x≤(-π/3)+2πk, k∈Z .
у=соsx убывает на (2πk;π+2πk), k∈Z
Решаем неравенство:
2πk ≤ x+(π/3)≤π +2πk, k∈Z
у=сos(x+(π/3)) убывает при
(-π/3)+2πk ≤x≤(2π/3)+2πk, k∈Z .
в) Решаем уравнение
сos(x+(π/3))=0
x+(π/3)=(π/2)+πn, n∈Z;
x=(π/2)-(π/3)+πn, n∈Z;
x=(π/6)+πn, n∈Z.