1.
Объем куба вычисляется по формуле:
V=a³
V=15³=3375 cм³
Поскольку шар переплавили из куба, то его объем равен объему куба:
V=4/3πr³=3375 см³
4/3πr³=3375
4/3*3.14*r³=3375
r³=3375*3/(4*3.14)
r³≈806.13
r≈9.3 cм радиус шара
2.
Объем шарового сегмента определяется по формуле:
V=πh²(R-1/3h)
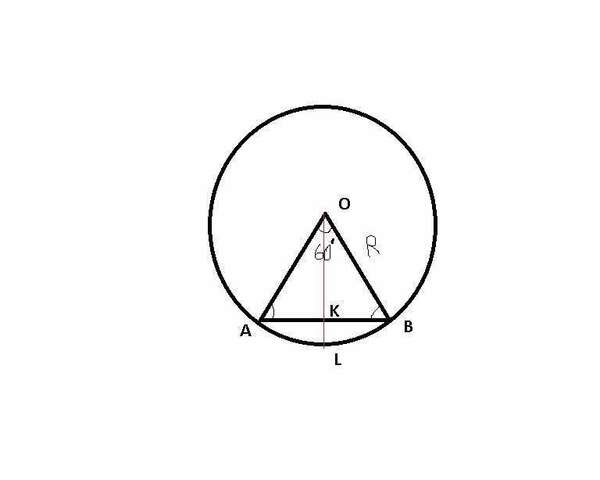
Рассмотрим треугольник полученный осевым сечением.
АОВ - равносторонний треугольник, ∠AOB=60°, АО=ОВ=R ⇒
АВ=R
OL=R
h=KL=OL-OK=R-OK
OK=R*sin 60=√3/2*R
h=R-√3/2R
V=πh²(R-1/3h)=π(R-√3/2R)²(R-1/3(R-√3/2R))=πr³(40-23√3)/24
3.
Площадь сечения равна:
S=πr²=81 cм²
r²=81/3.14
r≈5.1 cм
V=πh²(R-1/3h)
r²=R²-OK²
5.1²=15²-OK²
OK≈14.1 см
h=KL=OL-OK=R-OK=15-14,1=0,9
V=πh²(R-1/3h)=3,14*0,9²*(15-1/3*0,9)≈37,4 см³ площадь малого сегмента