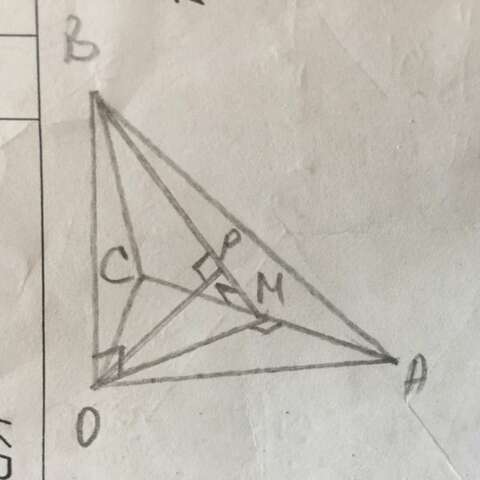
А) Треугольник АСО∈α, ВО⊥α,значит ВО⊥АС.
ВМ⊥АС и ВО⊥АС, значит по теореме о трёх перпендикулярах ОМ⊥АС, следовательно ∠ВМО - линейный угол двугранного угла ВАСО.
б) По условию ∠ОВМ=30° и ОР=3 СМ. ОР⊥ВМ.
В тр-ке ВОР катет ОР лежит напротив угла в 30°, значит ВО=2·ОР=6 см.
В тр-ке ВОМ ВМ=ВО/cos30=6·2/√3=4√3 см.
В правильном тр-ке АВС ВМ - высота.
ВМ=АВ√3/2 ⇒ АВ=2ВМ/√3=2·4√3/√3=8 см.
Площадь тр-ка АВС: S=АВ²√3/4=64√3/4=16√3 см² - это ответ.