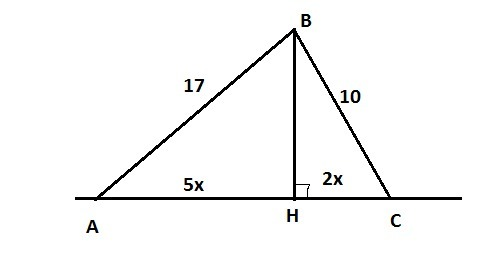
Пусть ВН - перпендикуляр к прямой АС, АВ=17 см - наклонная, ВС=10 см - наклонная, АН:НС=5:2.
Пусть х - коэффициент пропорциональности, тогда АН=5х, НС=2х.
Рассмотрим ΔАНВ - прямоугольный, по т.Пифагора ВН²=АВ²-АН²=
=17²-(5х)²=289-25х².
Рассмотрим ΔВНС - прямоугольный, по т.Пифагора ВН²=ВС²-НС²=
=10²-(2х)²=100-4х².
Приравниваем полученные выражения и находим х:
289-25х²=100-4х²;
25x²-4x²=289-100;
21x²=189;
x²=9;
x=3.
Находим ВН=√(100-4*3²)=√(100-36)=√64=8 (см).
Ответ: 8 см.