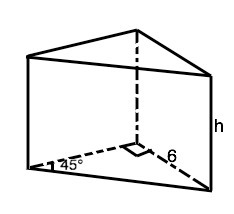
Если в прямоугольном треугольнике один из острых углов 45°, второй тоже 45°, и тогда его катеты равны. Гипотенуза равна катету, деленному на синус острого угла=  =6√2
=6√2
Объем призмы равен произведению площади ее основания на высоту.
V=S•h
Площадь прямоугольного треугольника в основании
S=а•b:2
S=6•6:2=18 см²
h=V:S
h=108:18=6 см
Площадь боковой поверхности прямой призмы равна сумме площадей ее боковых граней ( прямоугольников) или произведению высоты на периметр основания, что дает одинаковый результат.
S бок=h•P=6•(6+6+6√2)=6•6(2+√2)=36•(2+√2)см²