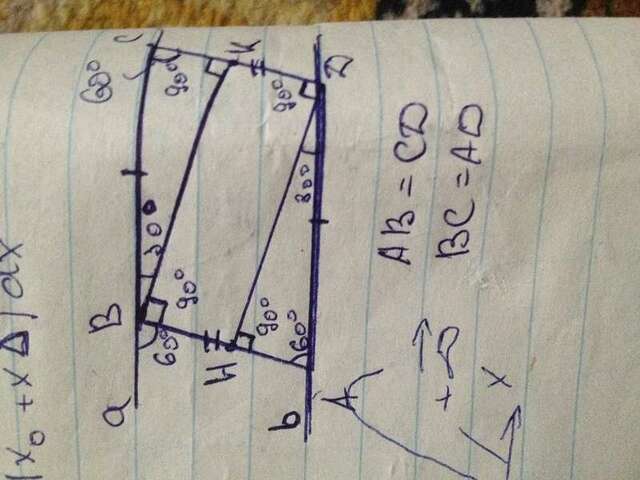
Два угла в параллелограмме можно доказать так,если учитель у вас не будет против и данное доказательство немного нестандартна,но чем смог,тем я помог.
Доказательство:
Рассмотрим параллелограмм и нам нужно доказать,что противоположные угла А и C равны!
Нам дано,что у параллелограмма есть четыре равные стороны,а именно АВ = СD и BC=AD значит : Проведём две линии(это не диагонали) от вершины В и D к сторонам АВ и СD,то есть от точки В линия идёт до СD,а от точки D до СD и при этом стороны поделились на неравные части,а точки деления обозначим Н-(это точка на стороне АВ) и К-(это точка СD),также образовались углы АВС и АDC равны 90 град. Далее, наблюдаем,что,так как ВC =AD,то они являются параллельными прямыми a и b и при этом образовались четыре внешних угла,смежные углам АВС,ВАD,ADC,BCD. Затем,найдём градусную меру внешнего угла смежный углом АВС и одновременно рассмотрим прямоугольный треугольник ВСK,который образовался путём проведения прямых внутри параллелограмма,затем свойство прямого. треугольника гласит,что сумма двух углов равна 90 градусов,можно сказать,что угол КВС соответственно равен 30 град,а это значит,что внешний угол,который смежный с углом АBC(можно проверить,что сумма трёх углов: внешний,АВD и KBC будет давать,по свойству смежных углов,180 град.) равен 60 градусам,то накрест лежащие углы равны,то есть внешний угол смежный с углом АВС равен углу ВАС!Также доказываем и с углом ВСD!Сделаем вывод,что угол DAB и ВСD равны 60 град.,то эти углы равны,что и требовалось доказать.