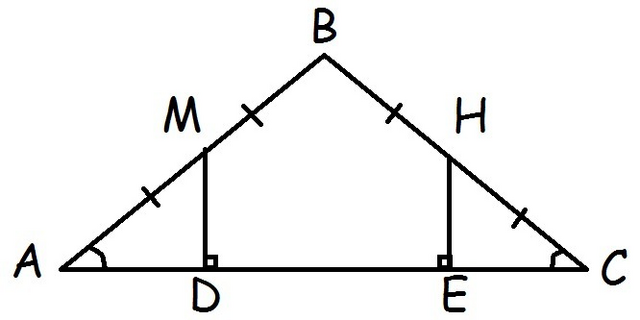
Если АВ = ВС, то треугольник АВС равнобедренный. Тогда угол ВСА = углу ВАС.
Если АВ = ВС, а точки М и Н - середины этих сторон, то АМ = МВ = СН = ВН.
Если MD и HE перпендикулярны к прямой AC, то тругольники МDА и НЕС - прямоугольные.
У треугольников МDА и НЕС:
1) Угол ВСА = углу ВАС
2) АМ = НС
За гипотенузой и катетом треугольник АМD = треугольнику СНЕ.