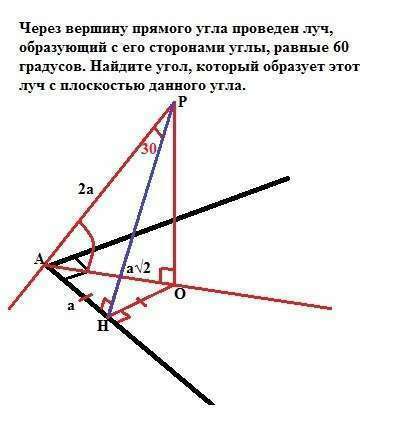
Поскольку прямая, проходящая через вершину угла, образует с его сторонами равные углы, значит проекция этой прямой на плоскость угла является его биссектрисой.
Возьмем на прямой точку Р и опустим из нее перпендикуляры РО на плоскость угла и РН на сторону этого угла. По теореме о трех перпендикулярах, отрезок ОН будет перпендикулярен стороне АН. Тогда в треугольнике АОН катеты АН и ОН равны (так как АО - биссектриса). Пусть они равны "а".
Тогда АО= а√2.
В прямоугольном треугольнике АРН угол РАН=60° (дано), тогда Значит АР =2а (так как катет АН лежит против угла 30°).
Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость.
То есть нам надо найти градусную меру угла РАО.
Косинус угла РАО=АО/АР или Cos(PAO)=a√2/2a=√2/2.
Следовательно, искомый угол равен arccos(√2/2) или 45°.
Ответ: 45°.