В кубе 6 граней (сторон),
Каждая грань разделена на 9 кубиков, обозначим из по порядку:
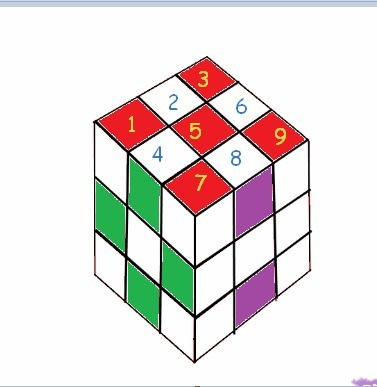
1 2 3 4 5 6 7 8 9 (см. рисунок).
В купе 3 пары противоположных граней:
пара 1 - верняя и нижняя грани, раскрасим 5кубиков под номерами 1 3 5 7 9,
пара 2 - передняя и задняя грани, раскрасим 4 кубика под номерами 2 4 6 8
пара 3 - боковые грани, раскрасим 2 кубика под номерами 2 и 8.
Ответ: 1. условие выполнено - раскрашенные кубики не имеют общих сторон.
2. 2*5+2*4+2*2=22
Самое большое количество кубиков, которое можео покрасить соответственно условию, равно 22.