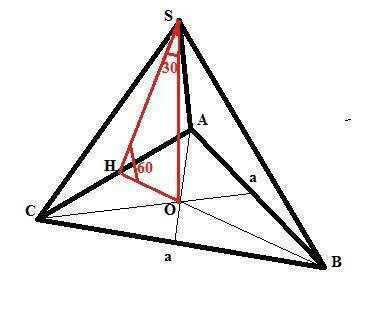
В правильной треугольной пирамиде основанием высоты является центр правильного треугольника.. Этот центр - пересечение высот, медиан и биссектрис треугольника.
Нам дано, что боковая грань правильной треугольной пирамиды образует с плоскостью основания угол в 60 градусов. Это значит, что апофема SН (высота боковой грани) образует с плоскостью основания угол 60 градусов.
В прямоугольном треугольнике ОSH: tg60=SO/OH.
Отсюда ОН=SO/tg60 или ОН= 10√3/√3 =10.
Этот отрезок можно найти и по Пифагору:
SH²-ОН²=SO², отсюда ОН=√(300/3)=10.
ОН - это 1/3 от высоты правильного треугольника (основания пирамиды), так как медианы треугольника делится точкой пересечения (центром правильного треугольника) в отношении 2:1, считая от вершины. Значит высота равна 30. Тогда сторона основания "a" найдется из формулы: h=(√3/2)*a:
а=2*h/√3 или а=20√3.
Ответ: сторона основания равна 20√3.