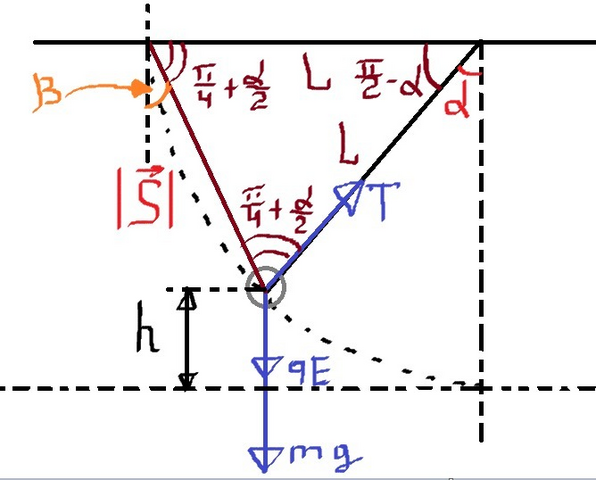
Так как вектор напряженности электрического поля направлен вертикально вниз, то условно мы можем считать, что сверху расположена положительно заряженная обкладка, а снизу - отрицательно
так как тело заряжено положительно, то оно будет притягиваться к отрицательно заряженной обкладке, т.е. сила F = q E со стороны электрического поля, действующая на тело, направлена вертикально вниз
электрическое поле способствует движению тела. с учетом этого запишем закон сохранения энергии:
mgL + q E S cosβ = (m v²)/2 + mgh,
где S - это модуль вектора перемещения тела (отрезок, соединяющий начальное и конечное положения), cosβ - угол между векторами силы и перемещения
из чертежа нетрудно получить, что
S = L
β = (π/2) - α
h = L (1 - cosα)
таким образом, ЗСЭ примет вид:
2 gL + 2 qE L sinα = v² + 2 gL (1 - cosα)
v² = 2 gL cosα + 2 qE L sinα
так как мы предполагаем, что нить не растяжима, то тело движется по окружности, поэтому оно в нужный нам момент обладает центростремительным ускорением a = v²/L, направленным вдоль нити. запишем уравнение динамики:
T - (mg + qE) cosα = m (v²/L)
T = mg cosα + qE cosα + 2 mg cosα + 2 mqE sinα
T = 3 mg cosα + q E cosα (1 + 2m tgα)
T = 300*0.866+5*10^(-6)*2*10^(3)*0.866*(1+20*0.577) ≈ 260 H